Bob要为NASA编写一个查找算法，这个算法在火箭即将登陆月球前开始执行，帮助计算着陆地点。

这个示例表明，两种算法的运行时间呈现不同的增速。 Bob需要做出决定，是使用简单查找还是二分查找。使用的算法必须快速而准确。一方面，二分查找的速度更快。 Bob必须在10秒钟内找出着陆地点，否则火箭将偏离方向。另一方面，简单查找算法编写起来更容易，因此出现bug的可能性更小。 Bob可不希望引导火箭着陆的代码中有bug！为确保万无一失，Bob决定计算两种算法在列表包含100个元素的情况下需要的时间。

假设检查一个元素需要1毫秒。使用简单查找时， Bob必须检查100个元素，因此需要100毫秒才能查找完毕。而使用二分查找时，只需检查7个元素（log2100大约为7），因此需要7毫秒就能查找完毕。然而，实际要查找的列表可能包含10亿个元素，在这种情况下，简单查找需要多长时间呢？二分查找又需要多长时间呢？请务必找出这两个问题的答案，再接着往下读。

Bob使用包含10亿个元素的列表运行二分查找，运行时间为30毫秒（log2 1000000000大约为30）。他心里想，二分查找的速度大约为简单查找的15倍，因为列表包含100个元素时，简单查找需要100毫秒，而二分查找需要7毫秒。因此， 列表包含10亿个元素时，简单查找需要30 × 15 = 450毫秒，完全符合在10秒内查找完毕的要求。 Bob决定使用简单查找。这是正确的选择吗？

不是。实际上， Bob错了，而且错得离谱。列表包含10亿个元素时，简单查找需要10亿毫秒，相当于11天！为什么会这样呢？因为二分查找和简单查找的运行时间的增速不同。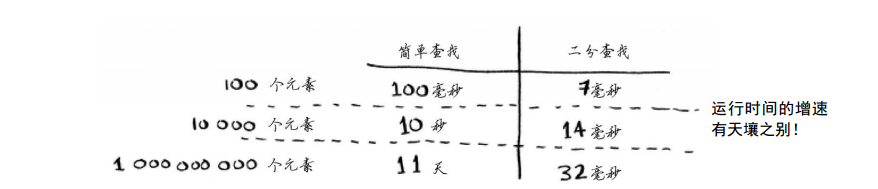也就是说，随着元素数量的增加，二分查找需要的额外时间并不多，而简单查找需要的额外时间却很多。因此，随着列表的增长，二分查找的速度比简单查找快得多。 Bob以为二分查找速度为简单查找的15倍，这不对：列表包含10亿个元素时，为3300万倍。有鉴于此，仅知道算法需要多长时间才能运行完毕还不够，还需知道运行时间如何随列表增长而增加。这正是大O表示法的用武之地。

大O表示法指出了算法有多快。例如，假设列表包含n个元素。简单查找需要检查每个元素，因此需要执行n次操作。使用大O表示法，这个运行时间为O(n)。单位秒呢？没有——大O表示法指的并非以秒为单位的速度。 大O表示法让你能够比较操作数，它指出了算法运行时间的增速。

再来看一个例子。为检查长度为n的列表，二分查找需要执行log n次操作。使用大O表示法，这个运行时间怎么表示呢？ O(log n)。

这指出了算法需要执行的操作数。之所以称为大O表示法，是因为操作数前有个大O。这听起来像笑话，但事实如此！

下面来看一些例子，看看你能否确定这些算法的运行时间。