本章内容

• 学习散列表——最有用的基本数据结构之一。散列表用途广泛，本章将介绍其常见的用途。
• 学习散列表的内部机制：实现、冲突和散列函数。这将帮助你理解如何分析散列表的性能

假设你在一家杂货店上班。有顾客来买东西时，你得在一个本子中查找价格。如果本子的内容不是按字母顺序排列的，你可能为查找苹果（apple）的价格而浏览每一行，这需要很长的时间。此时你使用的是第1章介绍的简单查找，需要浏览每一行。还记得这需要多长时间吗？ O(n)。如果本子的内容是按字母顺序排列的，可使用二分查找来找出苹果的价格，这需要的时间更短，为O(log n)。

需要提醒你的是，运行时间O(n)和O(log n)之间有天壤之别！假设你每秒能够看10行，使用简单查找和二分查找所需的时间将如下。

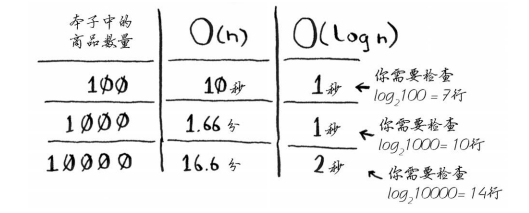
你知道， 二分查找的速度非常快。但作为收银员，在本子中查找价格是件很痛苦的事情，哪怕本子的内容是有序的。在查找价格时，你都能感觉到顾客的怒气。看来真的需要一名能够记住所有商品价格的雇员，这样你就不用查找了：问她就能马上知道答案。

不管商品有多少，这位雇员（假设她的名字为Maggie）报出任何商品的价格的时间都为O(1)，速度比二分查找都快。

真是太厉害了！如何聘到这样的雇员呢？

下面从数据结构的角度来看看。前面介绍了两种数据结构：数组和链表（其实还有栈，但栈并不能用于查找）。你可使用数组来实现记录商品价格的本子。

这种数组的每个元素包含两项内容：商品名和价格。如果将这个数组按商品名排序，就可使用二分查找在其中查找商品的价格。这样查找价格的时间将为O(log n)。然而，你希望查找商品价格的时间为O(1)，即你希望查找速度像Maggie那么快，这是散列函数的用武之地。