Jonah正为其虚构的橄榄球队挑选队员。他列了一个清单，指出了对球队的要求：优秀的四分卫，优秀的跑卫，擅长雨中作战，以及能承受压力等。他有一个候选球员名单，其中每个球员都满足某些要求。

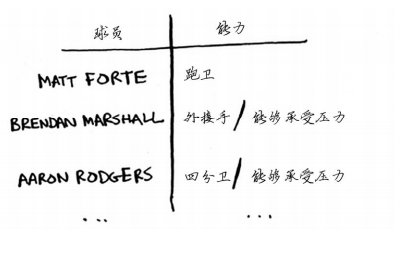
Jonah需要组建一个满足所有这些要求的球队，可名额有限。等等， Jonah突然间意识到，这不就是一个集合覆盖问题吗！

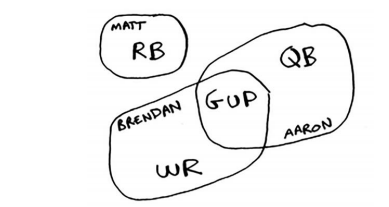
Jonah可使用前面介绍的近似算法来组建球队。

1. 找出符合最多要求的球员。
2. 不断重复这个过程，直到球队满足要求（或球队名额已满）。

NP完全问题无处不在！如果能够判断出要解决的问题属于NP完全问题就好了，这样就不用去寻找完美的解决方案，而是使用近似算法即可。但要判断问题是不是NP完全问题很难，易于解决的问题和NP完全问题的差别通常很小。例如，前一章深入讨论了最短路径，你知道如何找出从A点到B点的最短路径。

但如果要找出经由指定几个点的的最短路径，就是旅行商问题——NP完全问题。简言之，没办法判断问题是不是NP完全问题，但还是有一些蛛丝马迹可循的。

• 元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
• 涉及“所有组合”的问题通常是NP完全问题。
• 不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
• 如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，它可能就是NP完全问题。
• 如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题。
• 如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。