这里有必要提一提Diffie-Hellman算法，它以优雅的方式解决了一个古老的问题：如何对消息进行加密，以便只有收件人才能看懂呢？

最简单的方式是设计一种加密算法，如将a转换为1， b转换为2，以此类推。这样，如果我给你发送消息“ 4,15,7”，你就可将其转换为“ d,o,g”。但我们必须就加密算法达成一致，这种方式才可行。我们不能通过电子邮件来协商，因为可能有人拦截电子邮件，获悉加密算法，进而破译消息。即便通过会面来协商，这种加密算法也可能被猜出来——它并不复杂。因此，我们每天都得修改加密算法，但这样我们每天都得会面！

即便我们能够每天修改，像这样简单的加密算法也很容易使用蛮力攻击破解。假设我看到消息“ 9,6,13,13,1624,16,19,13,5”，如果使用加密算法a = 1、 b = 2等，转换结果将如下。

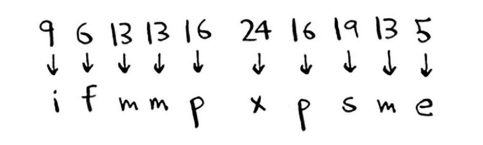
结果是一堆乱码。我们来尝试加密算法a = 2、 b = 3等。

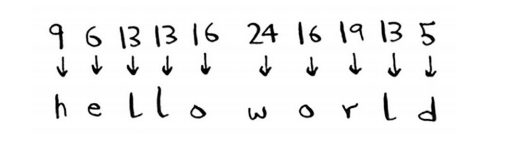
结果对了！像这样的简单加密算法很容易破解。在二战期间，德国人使用的加密算法比这复杂得多，但还是被破解了。 Diffie-Hellman算法解决了如下两个问题。

• 双方无需知道加密算法。他们不必会面协商要使用的加密算法。
• 要破解加密的消息比登天还难。

Diffie-Hellman使用两个密钥：公钥和私钥。顾名思义，公钥就是公开的，可将其发布到网站上，通过电子邮件发送给朋友，或使用其他任何方式来发布。你不必将它藏着掖着。有人要向你发送消息时，他使用公钥对其进行加密。加密后的消息只有使用私钥才能解密。只要只有你知道私钥，就只有你才能解密消息！

Diffie-Hellman算法及其替代者RSA依然被广泛使用。如果你对加密感兴趣，先着手研究Diffie-Hellman算法是不错的选择：它既优雅又不难理解。