假设有如下课程表,你希望将尽可能多的课程安排在某间教室上。
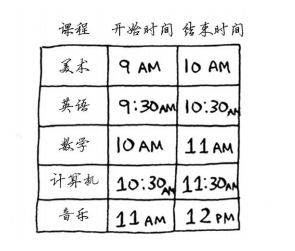
你没法让这些课都在这间教室上,因为有些课的上课时间有冲突。
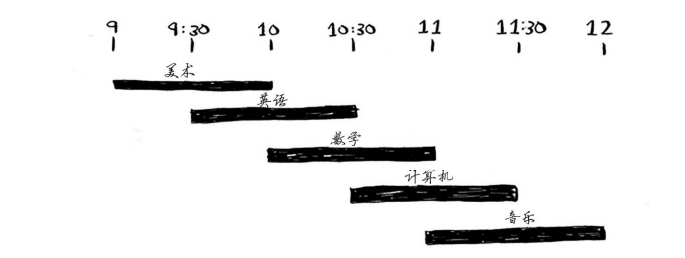
你希望在这间教室上尽可能多的课。如何选出尽可能多且时间不冲突的课程呢?
这个问题好像很难,不是吗?实际上,算法可能简单得让你大吃一惊。具体做法如下。
- 选出结束最早的课,它就是要在这间教室上的第一堂课。
- 接下来,必须选择第一堂课结束后才开始的课。同样,你选择结束最早的课,这将是要在这间教室上的第二堂课。
重复这样做就能找出答案!下面来试一试。美术课的结束时间最早,为10:00 a.m.,因此它就是第一堂课。
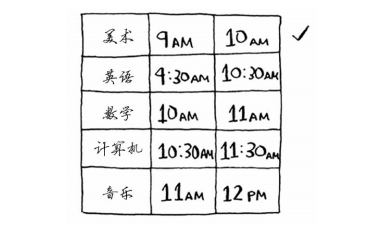
接下来的课必须在10:00 a.m.后开始,且结束得最早。
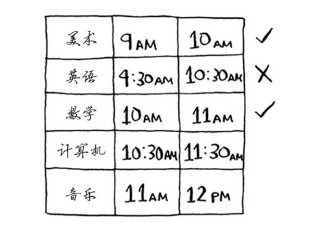
英语课不行,因为它的时间与美术课冲突,但数学课满足条件。最后,计算机课与数学课的 时间是冲突的,但音乐课可以。
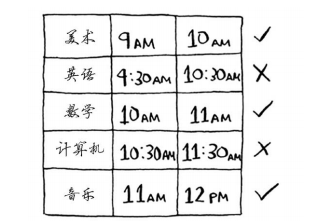
因此将在这间教室上如下三堂课。

很多人都跟我说,这个算法太容易、太显而易见,肯定不对。但这正是贪婪算法的优点——简单易行!贪婪算法很简单:每步都采取最优的做法。在这个示例中,你每次都选择结束最早的课。用专业术语说,就是你每步都选择局部最优解,最终得到的就是全局最优解。信不信由你,对于这个调度问题,上述简单算法找到的就是最优解!
显然,贪婪算法并非在任何情况下都行之有效,但它易于实现!下面再来看一个例子。