在前面的二分查找示例中，每当用户登录Facebook时， Facebook都必须在一个庞大的数组中查找，核实其中是否包含指定的用户名。前面说过，在这种数组中查找时，最快的方式是二分查找，但问题是每当有新用户注册时，都必须将其用户名插入该数组并重新排序，因为二分查找仅在数组有序时才管用。如果能将用户名插入到数组的正确位置就好了，这样就无需在插入后再排序。为此，有人设计了一种名为二叉查找树（binary search tree）的数据结构。

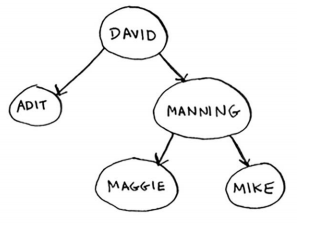
对于其中的每个节点，左子节点的值都比它小，而右子节点的值都比它大。

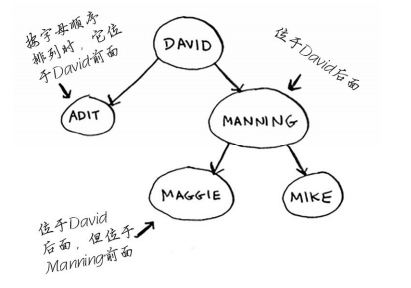
假设你要查找Maggie。为此，你首先检查根节点。

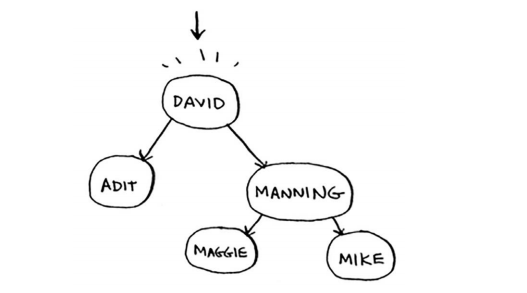
Maggie排在David的后面，因此你往右边找。

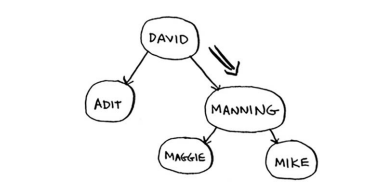
Maggie排在Manning前面，因此你往左边找。

终于找到了Maggie！这几乎与二分查找一样！在二叉查找树中查找节点时，平均运行时间为O(log n)，但在最糟的情况下所需时间为O(n)；而在有序数组中查找时，即便是在最糟情况下所需的时间也只有O(log n)，因此你可能认为有序数组比二叉查找树更佳。然而，二叉查找树的插入和删除操作的速度要快得多。

二叉查找树也存在一些缺点，例如，不能随机访问，就像不能这么说：“给我第五个元素。”在二叉查找树处于平衡状态时，平均访问时间也为O(log n)。假设二叉查找树像下面这样处于不平衡状态。

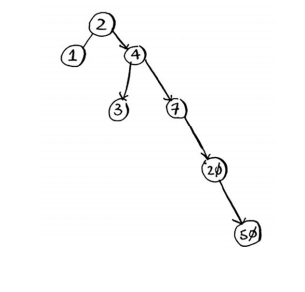
注意，这棵树是向右倾斜的，因此性能不佳。也有一些处于平衡状态的特殊二叉查找树，如红黑树。

那在什么情况下使用二叉查找树呢？ B树是一种特殊的二叉树，数据库常用它来存储数据。如果你对数据库或高级数据结构感兴趣，请研究如下数据结构： B树，红黑树，堆，伸展树。