我们从城市数较少的情况着手。假设只涉及两个城市，因此可供选择的路线有两条。

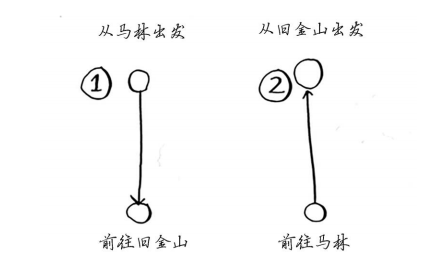
这两条路线相同还是不同

你可能认为这两条路线相同，难道从旧金山到马林的距离与从马林到旧金山的距离不同吗？不一定。有些城市（如旧金山）有很多单行线，因此你无法按原路返回。你可能需要离开原路行驶一两英里才能找到上高速的匝道。因此，这两条路线不一定相同。

你可能心存疑惑：在旅行商问题中，必须从特定的城市出发吗？例如，假设我是旅行商。我居住在旧金山，需要前往其他4个城市，因此我将从旧金山出发。

但有时候，不确定要从哪个城市出发。假设联邦快递将包裹从芝加哥发往湾区，包裹将通过航运发送到联邦快递在湾区的50个集散点之一，再装上经过不同配送点的卡车。该通过航运发送到哪个集散点呢？在这个例子中，起点就是未知的。因此，你需要通过计算为旅行商找出起点和最佳路线。

在这两种情况下，运行时间是相同的。但出发城市未定时更容易处理，因此这里以这种情况为例。

涉及两个城市时，可能的路线有两条。

3个城市

现在假设再增加一个城市，可能的路线有多少条呢？

如果从伯克利出发，就需前往另外两个城市。

从每个城市出发时，都有两条不同的路线，因此总共有6条路线。

因此涉及3个城市时，可能的路线有6条。

4个城市

我们再增加一个城市——弗里蒙特。现在假设从弗里蒙特出发。

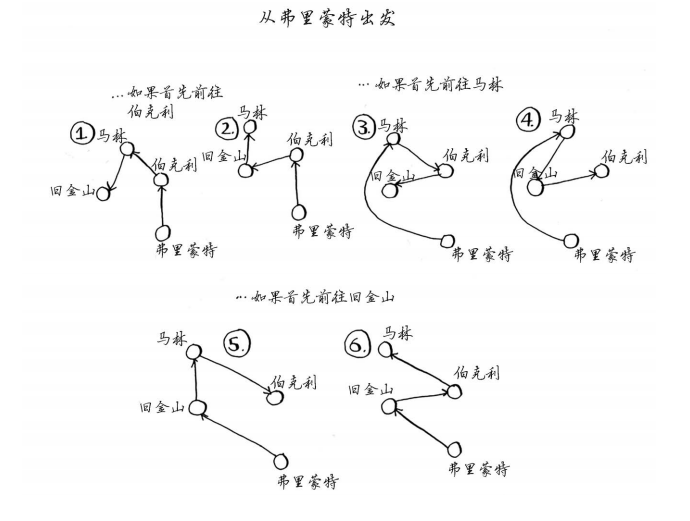
从弗里蒙特出发时，有6条可能的路线。这些路线与前面只有3个城市时计算的6条路线很像，只是现在所有的路线都多了一个城市——弗里蒙特！这里有一个规律。假设有4个城市，你选择一个出发城市——弗里蒙特后，还余下3个城市。而你知道，涉及3个城市时，可能的路线有6条。从弗里蒙特出发时，有6条可能的路线，但还可以从其他任何一个城市出发。

可能的出发城市有4个， 从每个城市出发时都有6条可能的路线，因此可能的路线有4 × 6 = 24条。

你看出规律了吗？每增加一个城市，需要计算的路线数都将增加。

涉及6个城市时，可能的路线有多少条呢？如果你说720条，那就对了。 7个城市为5040条， 8个城市为40 320条。

这被称为阶乘函数（factorial function） ，第3章介绍过。 5! = 120。假设有10个城市，可能的路线有多少条呢？ 10! = 3 628 800。换句话说，涉及10个城市时，需要计算的可能路线超过300万条。正如你看到的，可能的路线数增加得非常快！因此，如果涉及的城市很多，根本就无法找出旅行商问题的正确解。

旅行商问题和集合覆盖问题有一些共同之处：你需要计算所有的解，并从中选出最小/最短的那个。这两个问题都属于NP完全问题。

近似求解

对旅行商问题来说，什么样的近似算法不错呢？能找到较短路径的算法就算不错。在继续往下阅读前，看看你能设计出这样的算法吗？

我会采取这样的做法：随便选择出发城市，然后每次选择要去的下一个城市时，都选择还没去的最近的城市。

NP完全问题的简单定义是，以难解著称的问题，如旅行商问题和集合覆盖问题。很多非常聪明的人都认为，根本不可能编写出可快速解决这些问题的算法。