首先，需要使用代码来实现图。图由多个节点组成。

每个节点都与邻近节点相连，如果表示类似于“你→Bob”这样的关系呢？好在你知道的一种结构让你能够表示这种关系，它就是散列表！

记住，散列表让你能够将键映射到值。在这里，你要将节点映射到其所有邻居。

AMY : python的图实现是很有意思的，很是简洁优雅，但是如果想对图这种数据结构有更清晰的理解我觉得还是得看java或c++的实现更具代表性

表示这种映射关系的Python代码如下。

graph = {}
graph["you"] = ["alice", "bob", "claire"]

注意，“你”被映射到了一个数组，因此graph["you"]是一个数组，其中包含了“你”的所有邻居。

图不过是一系列的节点和边，因此在Python中，只需使用上述代码就可表示一个图。那像下面这样更大的图呢？

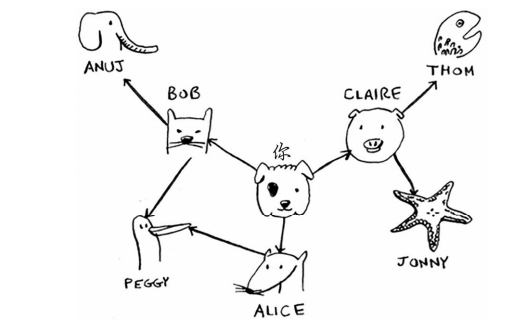
表示它的Python代码如下。

graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []

顺便问一句：键—值对的添加顺序重要吗？换言之，如果你这样编写代码：

graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []

而不是这样编写代码：

graph["anuj"] = []
graph["claire"] = ["thom", "jonny"]

对结果有影响吗？

只要回顾一下前一章介绍的内容，你就知道没影响。散列表是无序的，因此添加键—值对的顺序无关紧要。

Anuj、 Peggy、 Thom和Jonny都没有邻居，这是因为虽然有指向他们的箭头，但没有从他们出发指向其他人的箭头。这被称为有向图（directed graph） ，其中的关系是单向的。因此， Anuj是Bob的邻居，但Bob不是Anuj的邻居。 无向图（undirected graph）没有箭头，直接相连的节点互为邻居。例如，下面两个图是等价的。

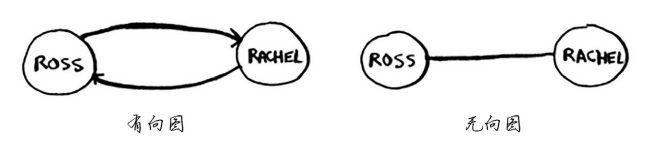
AMY ： 我认为这段描述是不严谨的，一个有向一个无向无论如何也不能称之为等价，意义不同。