递归函数也使用调用栈！来看看递归函数factorial的调用栈。 factorial(5)写作5!，其定义如下： 5! = 5 * 4 * 3 * 2 * 1。同理， factorial(3)为3 * 2 * 1。下面是计算阶乘的递归函数。

def fact(x):
    if x == 1:
        return 1
    else:
        return x * fact(x-1)

下面来详细分析调用fact(3)时调用栈是如何变化的。别忘了，栈顶的方框指出了当前执行到了什么地方。

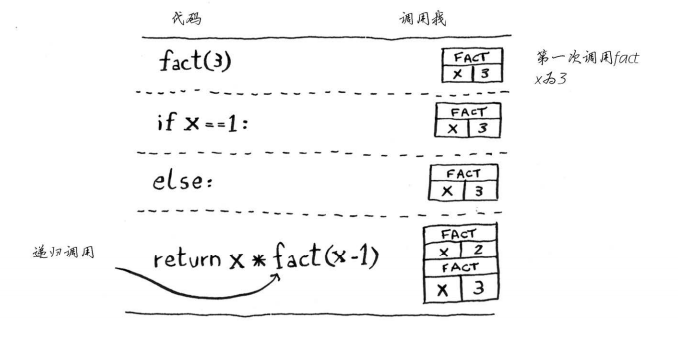
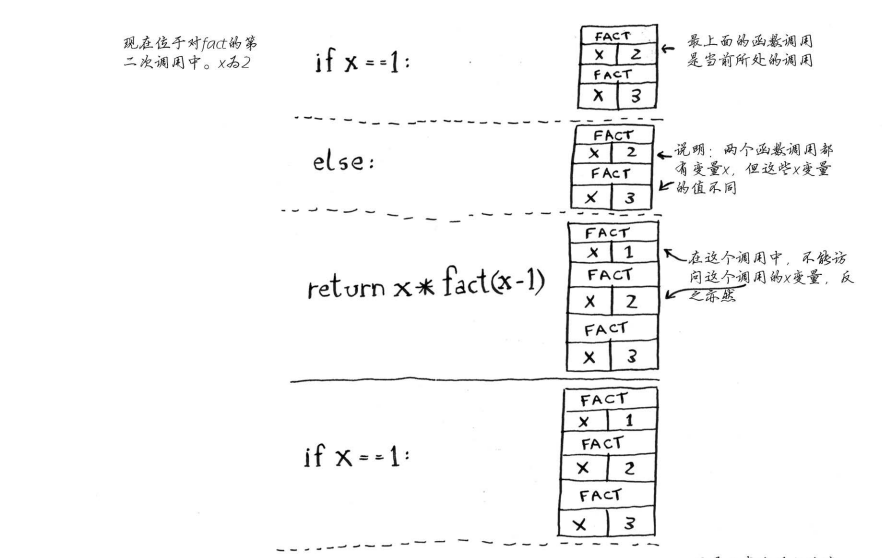
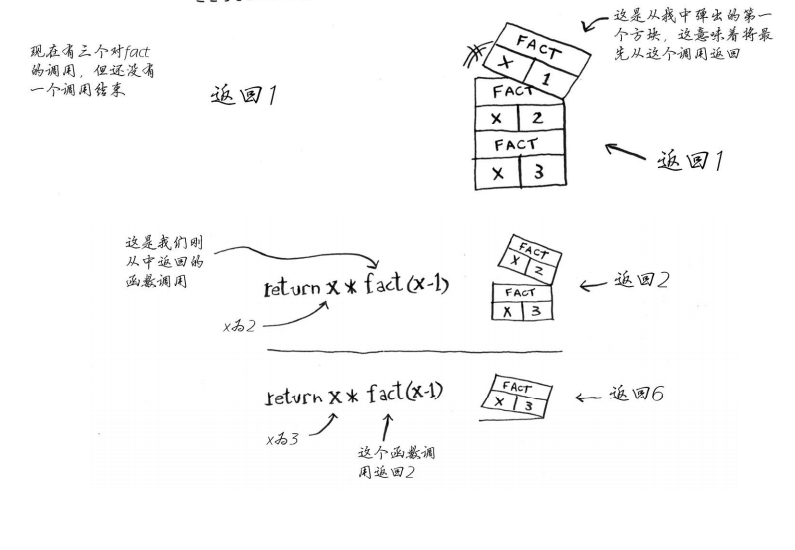
注意，每个fact调用都有自己的x变量。在一个函数调用中不能访问另一个的x变量。

栈在递归中扮演着重要角色。在本章开头的示例中，有两种寻找钥匙的方法。下面再次列出了第一种方法。

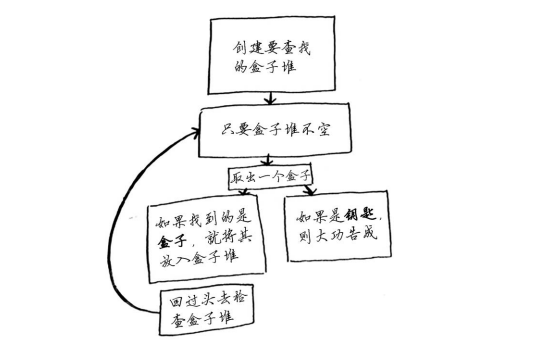
使用这种方法时，你创建一个待查找的盒子堆，因此你始终知道还有哪些盒子需要查找。

但使用递归方法时，没有盒子堆。

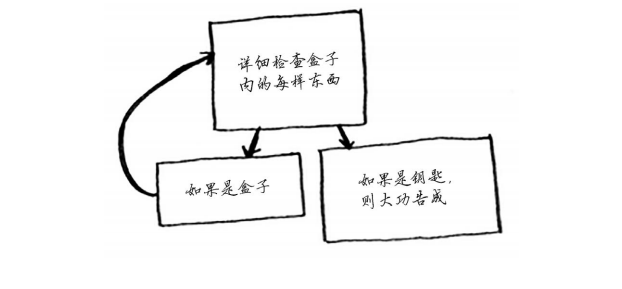
既然没有盒子堆，那算法怎么知道还有哪些盒子需要查找呢？下面是一个例子。

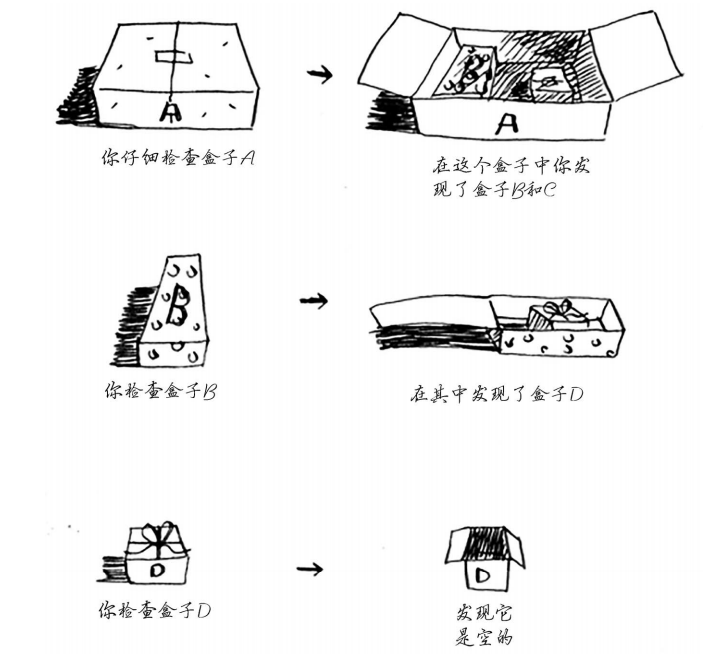
此时，调用栈类似于下面这样。

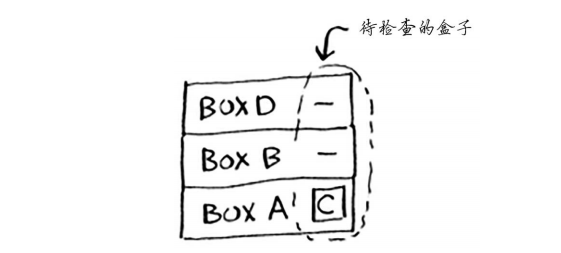
原来“盒子堆”存储在了栈中！这个栈包含未完成的函数调用，每个函数调用都包含还未检查完的盒子。使用栈很方便，因为你无需自己跟踪盒子堆——栈替你这样做了。

使用栈虽然很方便，但是也要付出代价：存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存，如果栈很高，就意味着计算机存储了大量函数调用的信息。在这种情况下，你有两种选择。

• 重新编写代码，转而使用循环。
• 使用尾递归。这是一个高级递归主题，不在本书的讨论范围内。另外，并非所有的语言都支持尾递归。