散列表的填装因子很容易计算。

散列表使用数组来存储数据，因此你需要计算数组中被占用的位置数。例如，下述散列表的填装因子为2/5，即0.4。

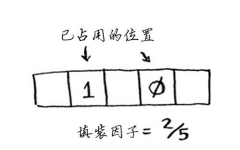
下面这个散列表的填装因子为多少呢？

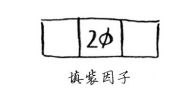
如果你的答案为1/3，那就对了。填装因子度量的是散列表中有多少位置是空的。

假设你要在散列表中存储100种商品的价格，而该散列表包含100个位置。那么在最佳情况下，每个商品都将有自己的位置。

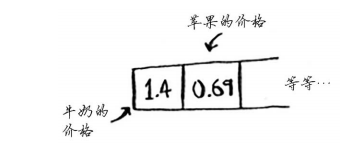
这个散列表的填装因子为1。如果这个散列表只有50个位置呢？填充因子将为2。不可能让每种商品都有自己的位置，因为没有足够的位置！填装因子大于1意味着商品数量超过了数组的位置数。一旦填装因子开始增大，你就需要在散列表中添加位置，这被称为调整长度（resizing） 。

例如，假设有一个像下面这样相当满的散列表。

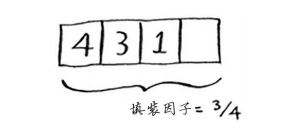
你就需要调整它的长度。为此，你首先创建一个更长的新数组：通常将数组增长一倍。

接下来， 你需要使用函数hash将所有的元素都插入到这个新的散列表中。

这个新散列表的填装因子为3/8，比原来低多了！填装因子越低，发生冲突的可能性越小，散列表的性能越高。一个不错的经验规则是：一旦填装因子大于0.7，就调整散列表的长度。

你可能在想，调整散列表长度的工作需要很长时间！你说得没错，调整长度的开销很大，因此你不会希望频繁地这样做。但平均而言，即便考虑到调整长度所需的时间，散列表操作所需的时间也为O(1)。