先概述一下这种算法的工作原理。
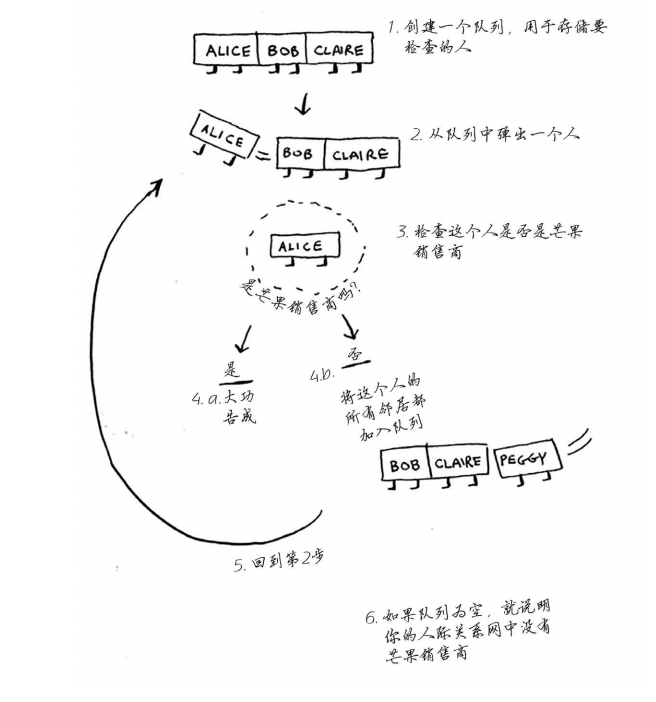
说 明
更新队列时,我使用术语“入队”和“出队”,但你也可能遇到术语“压入”和“弹出”。
压入大致相当于入队,而弹出大致相当于出队。
首先,创建一个队列。在Python中,可使用函数deque来创建一个双端队列。
from collections import deque
search_queue = deque()#创建一个队列
search_queue += graph["you"]#将你的邻居都加入到这个搜索队列中
别忘了, graph["you"]是一个数组,其中包含你的所有邻居,如["alice", "bob","claire"]。这些邻居都将加入到搜索队列中。
下面来看看其他的代码。
while search_queue:#只要队列不为空,
person = search_queue.popleft()#就取出其中的第一个人
if person_is_seller(person):#检查这个人是否是芒果销售商
print person + " is a mango seller!"#检查这个人是否是芒果销售商
return True
else:#不是芒果销售商。将这个人的朋友都加入搜索队列
search_queue += graph[person]
return False#如果到达了这里,就说明队列中没人是芒果销售商
最后,你还需编写函数person_is_seller,判断一个人是不是芒果销售商,如下所示。
def person_is_seller(name):
return name[-1] == 'm'
这个函数检查人的姓名是否以m结尾:如果是,他就是芒果销售商。这种判断方法有点搞笑,但就这个示例而言是可行的。下面来看看广度优先搜索的执行过程。
这个算法将不断执行,直到满足以下条件之一:
- 找到一位芒果销售商;
- 队列变成空的,这意味着你的人际关系网中没有芒果销售商。
Peggy既是Alice的朋友又是Bob的朋友,因此她将被加入队列两次:一次是在添加Alice的朋友时,另一次是在添加Bob的朋友时。因此,搜索队列将包含两个Peggy。

但你只需检查Peggy一次,看她是不是芒果销售商。如果你检查两次,就做了无用功。因此,检查完一个人后,应将其标记为已检查,且不再检查他。
如果不这样做,就可能会导致无限循环。假设你的人际关系网类似于下面这样。
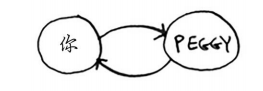
一开始, 搜索队列包含你的所有邻居。
现在你检查Peggy。她不是芒果销售商,因此你将其所有邻居都加入搜索队列。
接下来, 你检查自己。你不是芒果销售商,因此你将你的所有邻居都加入搜索队列。
以此类推。这将形成无限循环,因为搜索队列将在包含你和包含Peggy之间反复切换。

检查一个人之前,要确认之前没检查过他,这很重要。为此,你可使用一个列表来记录检查过的人。
考虑到这一点后,广度优先搜索的最终代码如下。
def search(name):
search_queue = deque()
search_queue += graph[name]
searched = []#这个数组用于记录检查过的人
while search_queue:
person = search_queue.popleft()
if not person in searched:#仅当这个人没检查过时才检查
if person_is_seller(person):
print person + " is a mango seller!"
return True
else:
search_queue += graph[person]
searched.append(person)#将这个人标记为检查过
return False
search("you")
请尝试运行这些代码,看看其输出是否符合预期。你也许应该将函数person_is_seller改为更有意义的名称。
运行时间
如果你在你的整个人际关系网中搜索芒果销售商,就意味着你将沿每条边前行(记住,边是从一个人到另一个人的箭头或连接),因此运行时间至少为O(边数)。
你还使用了一个队列,其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的,即为O(1),因此对每个人都这样做需要的总时间为O(人数)。所以,广度优先搜索的运行时间为O(人数 + 边数),这通常写作O(V + E),其中V为顶点(vertice)数, E为边数。