下面来看看如何使用代码来实现狄克斯特拉算法，这里以下面的图为例。

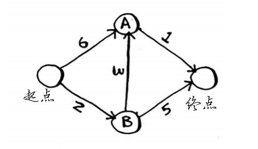
要编写解决这个问题的代码，需要三个散列表。

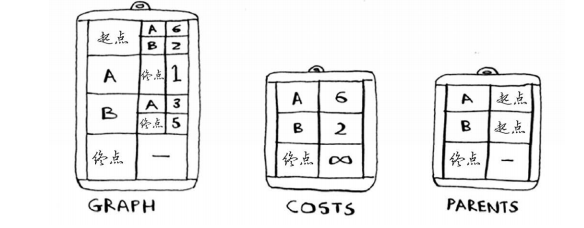
随着算法的进行，你将不断更新散列表costs和parents。首先，需要实现这个图，为此可像第6章那样使用一个散列表。

graph = {}

在前一章中，你像下面这样将节点的所有邻居都存储在散列表中。

graph["you"] = ["alice", "bob", "claire"]

但这里需要同时存储邻居和前往邻居的开销。例如，起点有两个邻居——A和B。

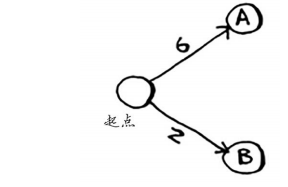
如何表示这些边的权重呢？为何不使用另一个散列表呢？

graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2

因此graph["start"]是一个散列表。要获取起点的所有邻居，可像下面这样做。

>>> print graph["start"].keys()
["a", "b"]

有一条从起点到A的边，还有一条从起点到B的边。要获悉这些边的权重，该如何办呢？

>>> print graph["start"]["a"]
2
>>> print graph["start"]["b"]
6

下面来添加其他节点及其邻居。

graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {} #终点没有任何邻居

表示整个图的散列表类似于下面这样。

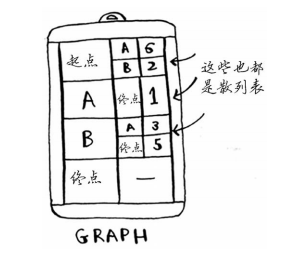
接下来， 需要用一个散列表来存储每个节点的开销。

节点的开销指的是从起点出发前往该节点需要多长时间。你知道的，从起点到节点B需要2分钟，从起点到节点A需要6分钟（但你可能会找到所需时间更短的路径）。你不知道到终点需要多长时间。对于还不知道的开销，你将其设置为无穷大。在Python中能够表示无穷大吗？你可以这样做：

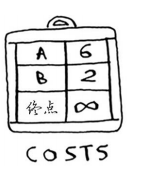
infinity = float("inf")

创建开销表的代码如下：

infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity

还需要一个存储父节点的散列表：

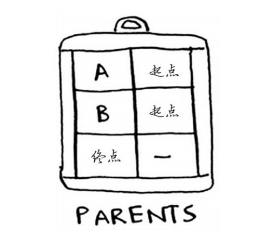
创建这个散列表的代码如下：

parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None

最后，你需要一个数组，用于记录处理过的节点，因为对于同一个节点，你不用处理多次。

processed = []

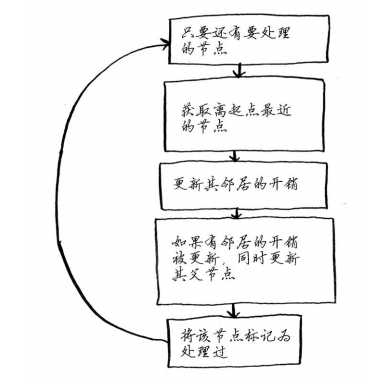
我先列出代码，然后再详细介绍。代码如下。

node = find_lowest_cost_node(costs)     #在未处理的节点中找出开销最小的节点
while node is not None:                 #这个while循环在所有节点都被处理过后结束
    cost = costs[node]
    neighbors = graph[node]
    for n in neighbors.keys():          #遍历当前节点的所有邻居
        new_cost = cost + neighbors[n]
        if costs[n] > new_cost:         #如果经当前节点前往该邻居更近，
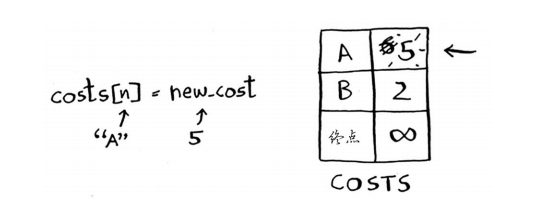
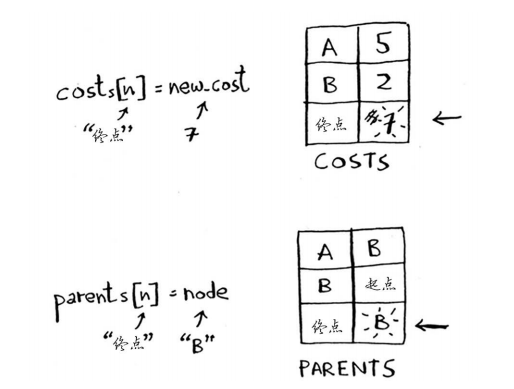
            costs[n] = new_cost         #就更新该邻居的开销
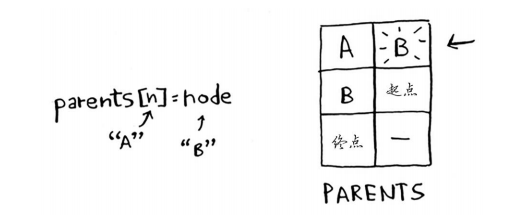
            parents[n] = node           #同时将该邻居的父节点设置为当前节点
    processed.append(node)              #将当前节点标记为处理过
    node = find_lowest_cost_node(costs) #找出接下来要处理的节点，并循环

这就是实现狄克斯特拉算法的Python代码！函数find_lowest_cost_node的代码稍后列出，我们先来看看这些代码的执行过程。

找出开销最低的节点。

获取该节点的开销和邻居。

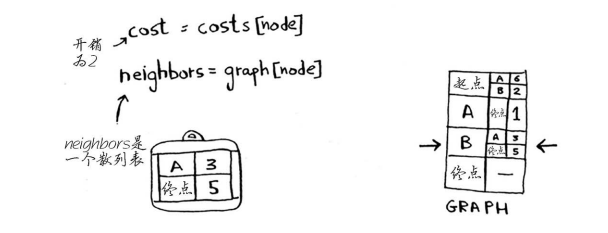
遍历邻居。

每个节点都有开销。开销指的是从起点前往该节点需要多长时间。在这里，你计算从起点出发，经节点B前往节点A（而不是直接前往节点A）需要多长时间。

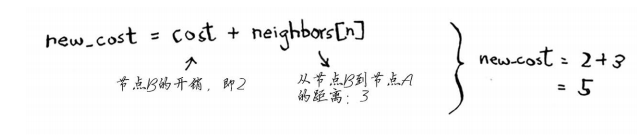
接下来对新旧开销进行比较。

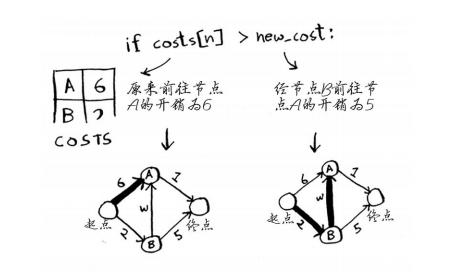
找到了一条前往节点A的更短路径！因此更新节点A的开销。

这条新路径经由节点B，因此节点A的父节点改为节点B。

现在回到了for循环开头。下一个邻居是终点节点。

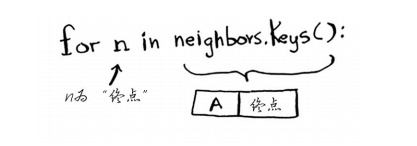
经节点B前往终点需要多长时间呢？

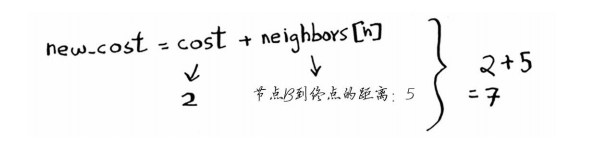
需要7分钟。终点原来的开销为无穷大，比7分钟长。

设置终点节点的开销和父节点。

你更新了节点B的所有邻居的开销。现在，将节点B标记为处理过。

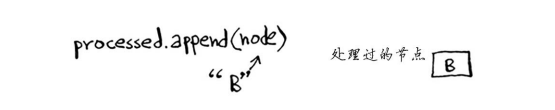
找出接下来要处理的节点。

获取节点A的开销和邻居。

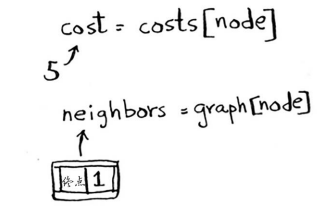
节点A只有一个邻居：终点节点。

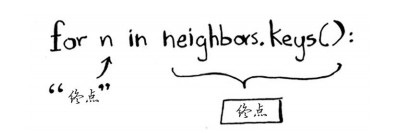
当前，前往终点需要7分钟。如果经节点A前往终点，需要多长时间呢？

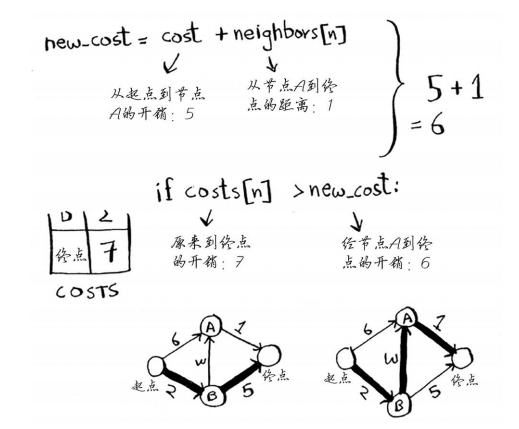
经节点A前往终点所需的时间更短！因此更新终点的开销和父节点。

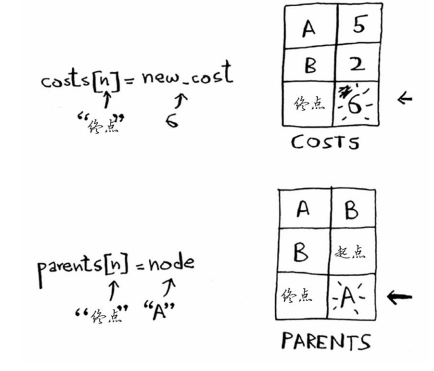
处理所有的节点后，这个算法就结束了。希望前面对执行过程的详细介绍让你对这个算法有更深入的认识。函数find_lowest_cost_node找出开销最低的节点，其代码非常简单，如下所示。

def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs:                                    #遍历所有的节点
        cost = costs[node]
        if cost < lowest_cost and node not in processed:  #如果当前节点的开销更低且未处理过，
            lowest_cost = cost                            #就将其视为开销最低的节点
            lowest_cost_node = node
return lowest_cost_node

AMY ： 书中实现的图和算法极为简易，实际上图是一种复杂的数据结构，实现起来较为复杂，建议有兴趣的朋友看看算法第四版中图的JAVA实现。

给个地址：https://algs4.cs.princeton.edu/home/

偷个懒这里就不标出具体在哪里了。