假设你不仅要向Priyanka推荐电影，还要预测她将给这部电影打多少分。为此，先找出与她最近的5个人。

顺便说一句，我老说最近的5个人，其实并非一定要选择5个最近的邻居，也可选择2个、 10个或10000个。这就是这种算法名为K最近邻而不是5最近邻的原因！

假设你要预测Priyanka会给电影Pitch Perfect打多少分。 Justin、 JC、 Joey、 Lance和Chris都给它打了多少分呢？

你求这些人打的分的平均值，结果为4.2。这就是回归（regression）。你将使用KNN来做两项基本工作——分类和回归：

• **分类就是编组； **
• 回归就是预测结果（如一个数字）。

回归很有用。假设你在伯克利开个小小的面包店，每天都做新鲜面包，需要根据如下一组特征预测当天该烤多少条面包：

• 天气指数1～5（1表示天气很糟， 5表示天气非常好）；
• 是不是周末或节假日（周末或节假日为1，否则为0）；
• 有没有活动（1表示有， 0表示没有）。

你还有一些历史数据，记录了在各种不同的日子里售出的面包数量。

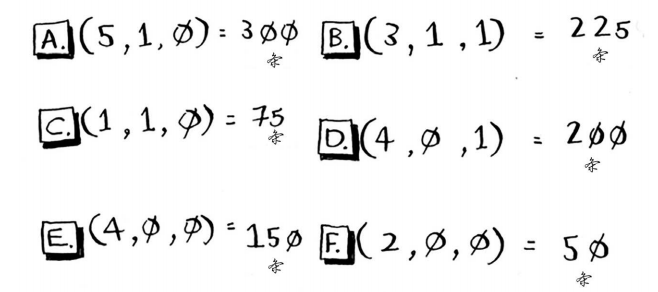
今天是周末，天气不错。根据这些数据，预测你今天能售出多少条面包呢？我们来使用KNN算法，其中的K为4。首先，找出与今天最接近的4个邻居。

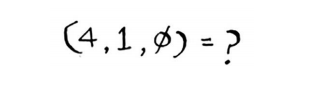
距离如下，因此最近的邻居为A、 B、 D和E。

将这些天售出的面包数平均，结果为218.75。这就是你今天要烤的面包数！

余弦相似度

前面计算两位用户的距离时，使用的都是距离公式。还有更合适的公式吗？在实际工作中，经常使用余弦相似度（cosine similarity） 。假设有两位品味类似的用户，但其中一位打分时更保守。他们都很喜欢Manmohan Desai的电影Amar Akbar Anthony，但Paul给了5星，而Rowan只给4星。如果你使用距离公式，这两位用户可能不是邻居，虽然他们的品味非常接近。

余弦相似度不计算两个矢量的距离，而比较它们的角度，因此更适合处理前面所说的情况。

本书不讨论余弦相似度，但如果你要使用KNN，就一定要研究研究它！