假设有下面这样打印列表中每个元素的简单函数。

def print_items(list):
    for item in list:
        print item

这个函数遍历列表中的每个元素并将其打印出来。它迭代整个列表一次，因此运行时间为O(n)。现在假设你对这个函数进行修改，使其在打印每个元素前都休眠1秒钟。

from time import sleep
def print_items2(list):
    for item in list:
        sleep(1)
        print item

它在打印每个元素前都暂停1秒钟。假设你使用这两个函数来打印一个包含5个元素的列表。

这两个函数都迭代整个列表一次，因此它们的运行时间都为O(n)。你认为哪个函数的速度更快呢？我认为print_items要快得多，因为它没有在每次打印元素前都暂停1秒钟。因此，虽然使用大O表示法表示时，这两个函数的速度相同，但实际上print_items的速度更快。在大O表示法O(n)中， n实际上指的是这样的。

c是算法所需的固定时间量，被称为常量。例如， print_ items所需的时间可能是10毫秒 *n，而print_items2所需的时间为1秒 * n。

通常不考虑这个常量，因为如果两种算法的大O运行时间不同，这种常量将无关紧要。就拿二分查找和简单查找来举例说明。假设这两种算法的运行时间包含如下常量。

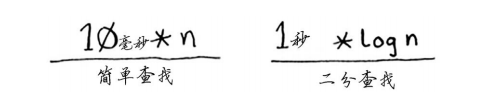
你可能认为，简单查找的常量为10毫秒，而二分查找的常量为1秒，因此简单查找的速度要快得多。现在假设你要在包含40亿个元素的列表中查找，所需时间将如下。

AMY : 算法导论对此有过详细的解释。

正如你看到的，二分查找的速度还是快得多，常量根本没有什么影响。

但有时候，常量的影响可能很大，对快速查找和合并查找来说就是如此。快速查找的常量比合并查找小，因此如果它们的运行时间都为O(n log n)，快速查找的速度将更快。实际上，快速查找的速度确实更快，因为相对于遇上最糟情况，它遇上平均情况的可能性要大得多。

此时你可能会问，何为平均情况，何为最糟情况呢？