术语介绍得差不多了，我们再来看一个例子！这是Rama，想拿一本乐谱换架钢琴。

Alex说：“这是我最喜欢的乐队Destroyer的海报，我愿意拿它换你的乐谱。如果你再加5美元，还可拿乐谱换我这张稀有的Rick Astley黑胶唱片。” Amy说：“哇，我听说这张黑胶唱片里有首非常好听的歌曲，我愿意拿我的吉他或架子鼓换这张海报或黑胶唱片。

Beethoven惊呼：“我一直想要吉他，我愿意拿我的钢琴换Amy的吉他或架子鼓。”

太好了！只要再花一点点钱， Rama就能拿乐谱换架钢琴。现在他需要确定的是，如何花最少的钱实现这个目标。我们来绘制一个图，列出大家的交换意愿。

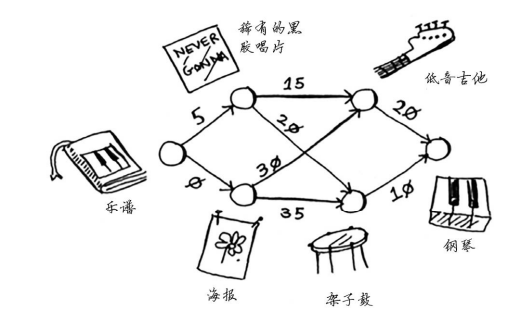
这个图中的节点是大家愿意拿出来交换的东西，边的权重是交换时需要额外加多少钱。拿海报换吉他需要额外加30美元，拿黑胶唱片换吉他需要额外加15美元。 Rama需要确定采用哪种路径将乐谱换成钢琴时需要支付的额外费用最少。为此，可以使用狄克斯特拉算法！别忘了，狄克斯特拉算法包含四个步骤。在这个示例中，你将完成所有这些步骤，因此你也将计算最终路径。

动手之前，你需要做些准备工作：创建一个表格，在其中列出每个节点的开销。这里的开销指的是达到节点需要额外支付多少钱。

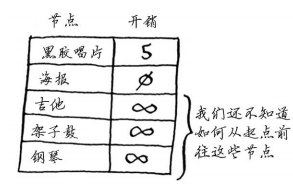
在执行狄克斯特拉算法的过程中，你将不断更新这个表。为计算最终路径，还需在这个表中添加表示父节点的列。

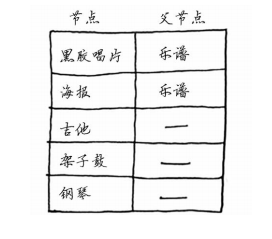
这列的作用将稍后介绍。我们开始执行算法吧。

第一步：

找出最便宜的节点。在这里，换海报最便宜，不需要支付额外的费用。还有更便宜的换海报的途径吗？这一点非常重要，你一定要想一想。 Rama能够通过一系列交换得到海报，还能额外得到钱吗？想清楚后接着往下读。答案是不能， 因为海报是Rama能够到达的最便宜的节点，没法再便宜了。

下面提供了另一种思考角度。假设你要从家里去单位。

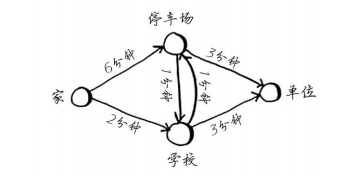
如果你走经过学校的路，到学校需要2分钟。 如果你走经过停车场的路，到停车场需要6分钟。如果经停车场前往学校，能不能将时间缩短到少于2分钟呢？不可能，因为只前往停车场就超过2分钟了。另一方面，有没有能更快到达停车场的路呢？有。

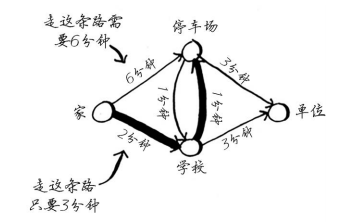
这就是狄克斯特拉算法背后的关键理念： 找出图中最便宜的节点，并确保没有到该节点的更便宜的路径！

回到换钢琴的例子。换海报需要支付的额外费用最少。

第二步：

计算前往该节点的各个邻居的开销。

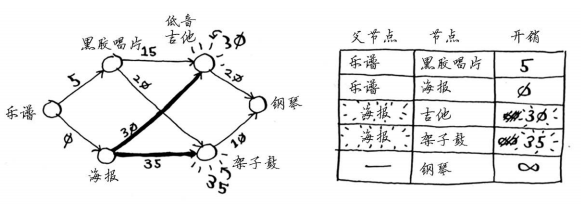
现在的表中包含低音吉他和架子鼓的开销。这些开销是用海报交换它们时需要支付的额外费用，因此父节点为海报。这意味着，要到达低音吉他，需要沿从海报出发的边前行，对架子鼓来说亦如此。

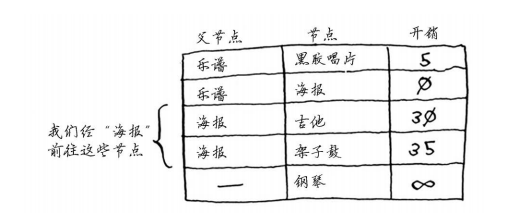
再次执行第一步：下一个最便宜的节点是黑胶唱片——需要额外支付5美元。

再次执行第二步：更新黑胶唱片的各个邻居的开销。

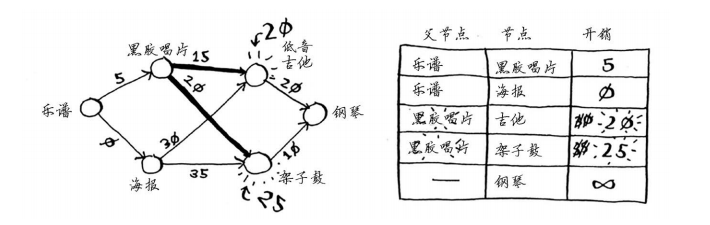
你更新了架子鼓和吉他的开销！这意味着经“黑胶唱片”前往“架子鼓”和“吉他”的开销更低，因此你将这些乐器的父节点改为黑胶唱片。

下一个最便宜的是吉他，因此更新其邻居的开销。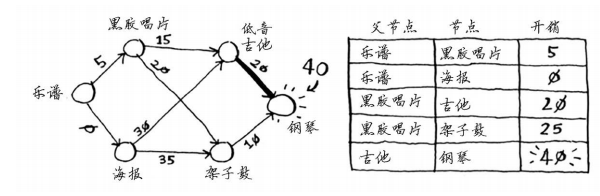

你终于计算出了用吉他换钢琴的开销，于是你将其父节点设置为吉他。最后，对最后一个节点——架子鼓，做同样的处理。

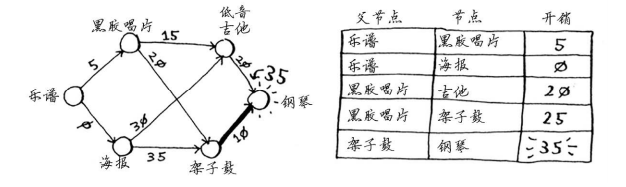
如果用架子鼓换钢琴， Rama需要额外支付的费用更少。因此， 采用最便宜的交换路径时，Rama需要额外支付35美元。

现在来兑现前面的承诺，确定最终的路径。当前，我们知道最短路径的开销为35美元，但如何确定这条路径呢？为此，先找出钢琴的父节点。

钢琴的父节点为架子鼓，这意味着Rama需要用架子鼓来换钢琴。因此你就沿着这一边。

我们来看看需要沿哪些边前行。 钢琴的父节点为架子鼓。

架子鼓的父节点为黑胶唱片。

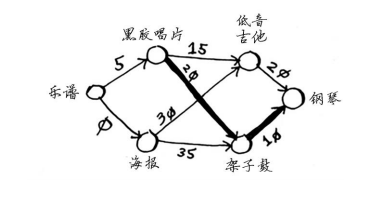
因此Rama需要用黑胶唱片了换架子鼓。显然，他需要用乐谱来换黑胶唱片。通过沿父节点回溯，便得到了完整的交换路径。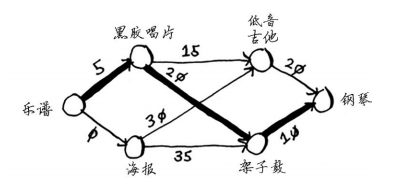

下面是Rama需要做的一系列交换。

本章前面使用的都是术语最短路径的字面意思：计算两点或两人之间的最短路径。但希望这个示例让你明白：最短路径指的并不一定是物理距离，也可能是让某种度量指标最小。在这个示例中，最短路径指的是Rama想要额外支付的费用最少。这都要归功于狄克斯特拉！