下面是一种更佳的猜法。从 50 开始。

小了，但排除了一半的数字！至此，你知道1～50都小了。接下来，你猜75。

大了， 那余下的数字又排除了一半！使用二分查找时，你猜测的是中间的数字，从而每次都
将余下的数字排除一半。接下来，你猜63（50和75中间的数字）

这就是二分查找，你学习了第一种算法！每次猜测排除的数字个数如下。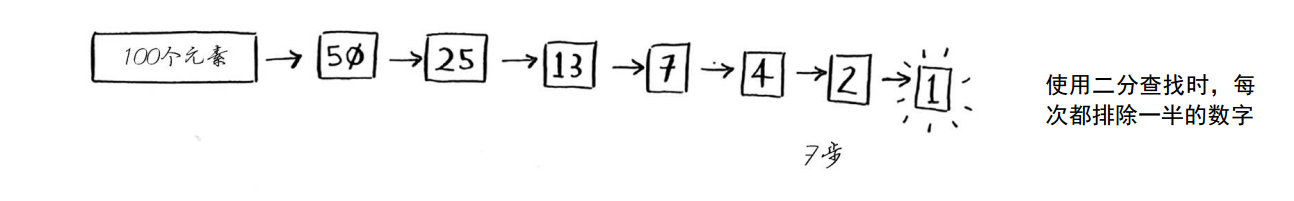
不管我心里想的是哪个数字，你在7次之内都能猜到，因为每次猜测都将排除很多数字！

假设你要在字典中查找一个单词，而该字典包含240 000个单词，你认为每种查找最多需要多少步？

如果要查找的单词位于字典末尾，使用简单查找将需要240 000步。使用二分查找时，每次排除一半单词，直到最后只剩下一个单词。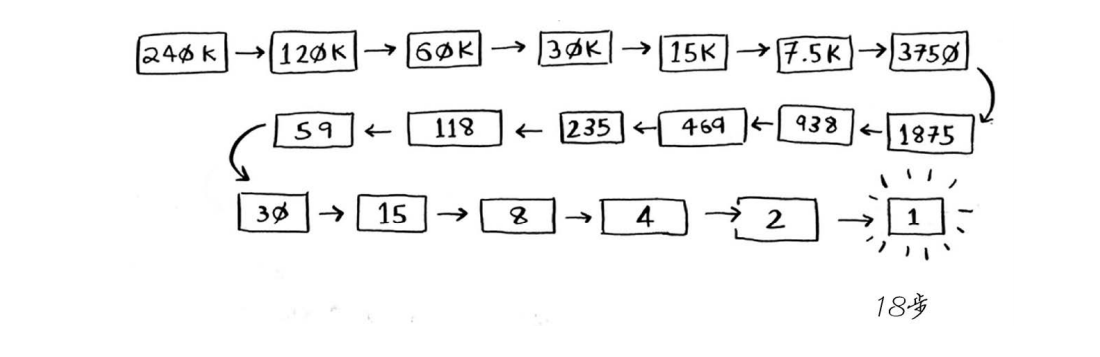因此，使用二分查找只需18步——少多了！一般而言，对于包含n个元素的列表，用二分查找最多需要log2n步，而简单查找最多需要n步。

对数

你可能不记得什么是对数了，但很可能记得什么是幂。 log10 100相当于问“将多少个10相乘的结果为100”。答案是两个： 10 × 10 = 100。因此， log10 100 = 2。对数运算是幂运算的逆运算。本书使用大O表示法（稍后介绍）讨论运行时间时， log指的都是log2。使用简单查找法查找元素时，在最糟情况下需要查看每个元素。因此，如果列表包含8个数字，你最多需要检查8个数字。而使用二分查找时，最多需要检查log n个元素。如果列表包含8个元素，你最多需要检查3个元素，因为log 8 = 3（23 = 8）。如果列表包含1024个元素，你最多需要检查10个元素，因为log 1024 = 10（210 =1024）。

说明：本书经常会谈到log时间，因此你必须明白对数的概念。如果你不明白，可汗学院
（khanacademy.org）有一个不错的视频，把这个概念讲得很清楚。

说明：仅当列表是有序的时候，二分查找才管用。例如，电话簿中的名字是按字母顺序排列的，
因此可以使用二分查找来查找名字。如果名字不是按顺序排列的，结果将如何呢？

下面来看看如何编写执行二分查找的Python代码。这里的代码示例使用了数组。如果你不熟悉数组，也不用担心，下一章就会介绍。你只需知道，可将一系列元素存储在一系列相邻的桶（bucket） ，即数组中。这些桶从0开始编号：第一个桶的位置为#0，第二个桶为#1，第三个桶为#2，以此类推 :

函数binary_search接受一个有序数组和一个元素。如果指定的元素包含在数组中，这个函数将返回其位置。你将跟踪要在其中查找的数组部分——开始时为整个数组。

def binary_search(list,item):
    low = 0
    high = len(list) - 1

    while (low <= high) :
        mid = low + high
        guess = list[mid]
        if guess == item :
            return mid
        if guess > item :
            high = mid -1
        else :
            low = mid + 1
    return None

my_list = [1,3,6,7,8,9]

print binary_search(my_list,6)
print binary_search(my_list,-1)