在前面的交换示例中， Alex提供了两种可用乐谱交换的东西。

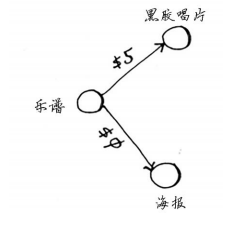
假设黑胶唱片不是Alex的，而是Sarah的，且Sarah愿意用黑胶唱片和7美元换海报。换句话说，换得Alex的海报后， Rama用它来换Sarah的黑胶唱片时，不但不用支付额外的费用，还可得7美元。对于这种情况，如何在图中表示出来呢？

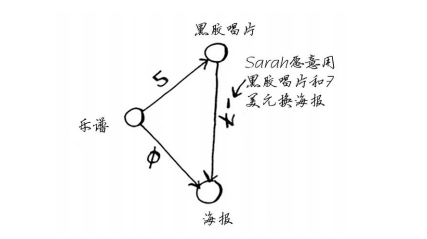
从黑胶唱片到海报的边的权重为负！即这种交换让Rama能够得到7美元。现在， Rama有两种获得海报的方式。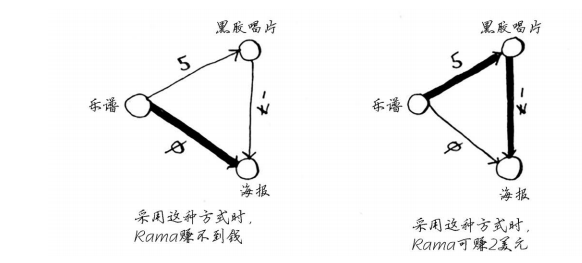

第二种方式更划算——Rama可赚2美元！你可能还记得， Rama可以用海报换架子鼓，但现在有两种换得架子鼓的方式。

第二种方式的开销少2美元，他应采取这种方式。然而，如果你对这个图运行狄克斯特拉算法， Rama将选择错误的路径——更长的那条路径。 如果有负权边，就不能使用狄克斯特拉算法。因为负权边会导致这种算法不管用。下面来看看对这个图执行狄克斯特拉算法的情况。首先，创建开销表。

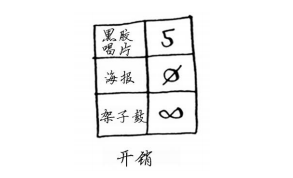
接下来， 找出开销最低的节点，并更新其邻居的开销。在这里，开销最低的节点是海报。根据狄克斯特拉算法， 没有比不支付任何费用获得海报更便宜的方式。（你知道这并不对！）无论如何，我们来更新其邻居的开销。

现在，架子鼓的开销变成了35美元。

我们来找出最便宜的未处理节点。

更新其邻居的开销。

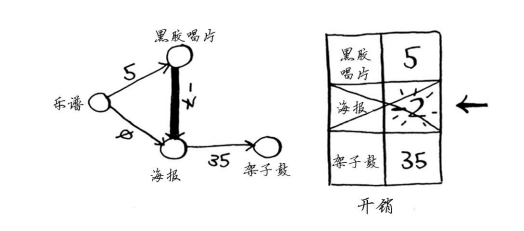
海报节点已处理过，这里却更新了它的开销。这是一个危险信号。节点一旦被处理，就意味着没有前往该节点的更便宜途径，但你刚才却找到了前往海报节点的更便宜途径！架子鼓没有任何邻居，因此算法到此结束，最终开销如下。

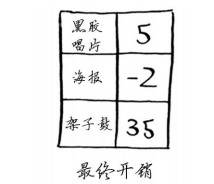
换得架子鼓的开销为35美元。你知道有一种交换方式只需33美元，但狄克斯特拉算法没有找到。这是因为狄克斯特拉算法这样假设：对于处理过的海报节点，没有前往该节点的更短路径。这种假设仅在没有负权边时才成立。因此， 不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中，要找出最短路径，可使用另一种算法——贝尔曼福德算法（Bellman-Ford algorithm）。本书不介绍这种算法，你可以在网上找到其详尽的说明。