下面来看看如何对下面的图使用这种算法。
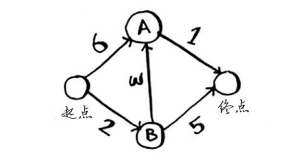
其中每个数字表示的都是时间,单位分钟。为找出从起点到终点耗时最短的路径,你将使用狄克斯特拉算法。
如果你使用广度优先搜索,将得到下面这条段数最少的路径。

这条路径耗时7分钟。下面来看看能否找到耗时更短的路径!狄克斯特拉算法包含4个步骤。
- 找出“最便宜”的节点,即可在最短时间内到达的节点。
- 更新该节点的邻居的开销,其含义将稍后介绍。
- 重复这个过程,直到对图中的每个节点都这样做了。
- 计算最终路径。
第一步:
找出最便宜的节点。你站在起点,不知道该前往节点A还是前往节点B。前往这两个节点都要多长时间呢?
前往节点A需要6分钟,而前往节点B需要2分钟。至于前往其他节点,你还不知道需要多长时间。
由于你还不知道前往终点需要多长时间,因此你假设为无穷大(这样做的原因你马上就会明白)。节点B是最近的——2分钟就能达到。
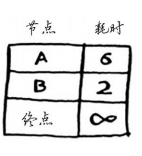
第二步:
计算经节点B前往其各个邻居所需的时间。
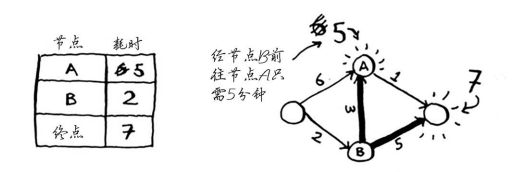
你刚找到了一条前往节点A的更短路径!直接前往节点A需要6分钟。
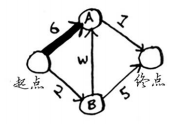
但经由节点B前往节点A只需5分钟!
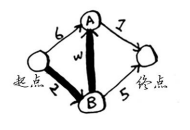
对于节点B的邻居,如果找到前往它的更短路径,就更新其开销。在这里,你找到了:
- 前往节点A的更短路径(时间从6分钟缩短到5分钟);
- 前往终点的更短路径(时间从无穷大缩短到7分钟)。
第三步:
重复第一步: 找出可在最短时间内前往的节点。你对节点B执行了第二步,除节点B外,可在最短时间内前往的节点是节点A。
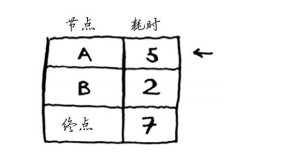
重复第二步:更新节点A的所有邻居的开销。
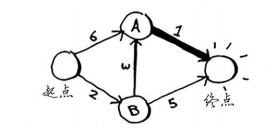
你发现前往终点的时间为6分钟!
你对每个节点都运行了狄克斯特拉算法(无需对终点这样做)。现在,你知道:
- 前往节点B需要2分钟;
- 前往节点A需要5分钟;
- 前往终点需要6分钟。

最后一步——计算最终路径将留到下一节去介绍,这里先直接将最终路径告诉你。
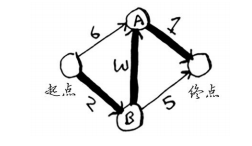
如果使用广度优先搜索,找到的最短路径将不是这条,因为这条路径包含3段,而有一条从起点到终点的路径只有两段。
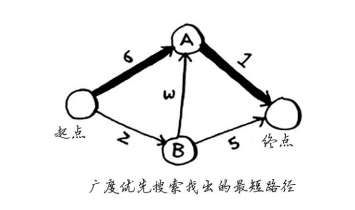
在前一章, 你使用了广度优先搜索来查找两点之间的最短路径,那时“最短路径”的意思是段数最少。在狄克斯特拉算法中,你给每段都分配了一个数字或权重,因此狄克斯特拉算法找出的是总权重最小的路径。
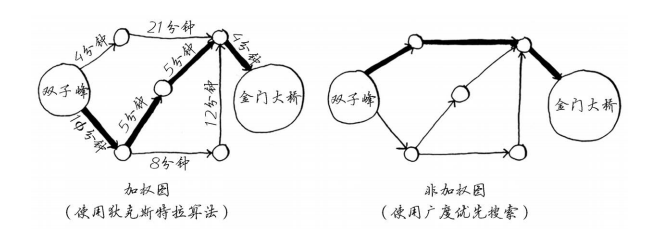
这里重述一下,狄克斯特拉算法包含4个步骤。
- 找出最便宜的节点,即可在最短时间内前往的节点。
- 对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。
- 重复这个过程,直到对图中的每个节点都这样做了。
- 计算最终路径。(下一节再介绍!)